Bitcoin Taproot

Intro: Bitcoin

Taproot is the first upgrade to Bitcoin in 4 years, since SegWit¹.

It is a softfork, meaning a backward-compatible upgrade. Nodes which do not upgrade to Taproot won't be able to use the new features though. Taproot includes 3 Bitcoin Improvement Proposals (BIPs):

1. BIP340: Schnorr Signatures
2. BIP341: Taproot
3. BIP342: Tapscript

Digital Signatures

Wikipedia's definition: a digital signature is a mathematical scheme for demonstrating the authenticity of a digital message or documents. A valid digital signature gives a recipient reason to believe that the message was created by a known sender (authentication), that the sender cannot deny having sent the message (nonrepudiation), and that the message was not altered in transit (integrity).

In Bitcoin:

• digital message is a transaction
• known sender is an owner of the private key k

A digital signature is a proof of owning a private key or knowledge of a number and the authenticity of intent to transfer the cryptocurrency.

Elliptic Curve Digital Signature Algorithm

Bitcoin uses ECDSA which was chosen by Satoshi in the past.

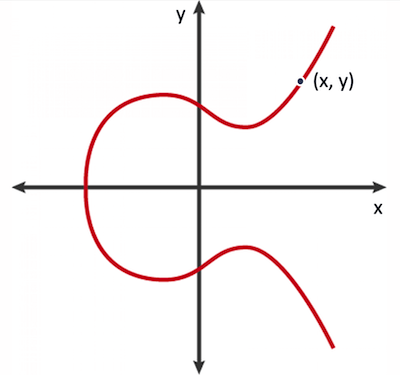
Elliptic curve is a graph on a pane, each point on a graph has x and y coordinates.
Let's agree that an uppercased letter is a point on a curve, and a lowercased letter is a regular number. There are 2 important properties:

• A + B = C — if two curve points A and B are added together, it produces a new curve point C
• A*n = B — if a curve point A is multiplied by a number n, it produces a new curve point B

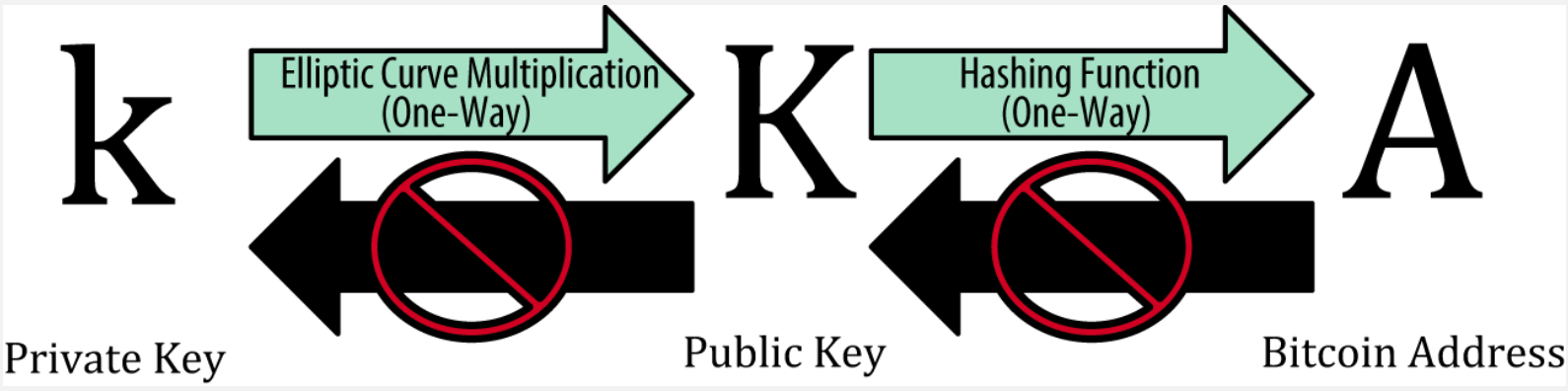
Elliptic Curve Multiplication on the picture means

• K = k*G, where G is called a Generator point and is publicly known. Multiplying it by a private key k, which is simply a big number, we produce a public key K. Elliptic curve division is infeasible, that's why knowing a public key K and G it is not possible to get the private key k.

1. BIP340: Schnorr Signatures

The main reason Satishi did not originally use Schnorr signatures is that Schnorr was not standardized, and was not available in common crypto libraries.

Nevertheless Schnorr signatures have many added advantages over ECDSA:

1. Schnorr signatures are provably secure. They are strongly unforgeable under chosen message attack (SUF-CMA). In contrast, the best known results for the provable security of ECDSA rely on stronger assumptions.
2. Non-malleability: The SUF-CMA security of Schnorr signatures implies that they are non-malleable. On the other hand, ECDSA signatures are inherently malleable: a third party without access to the secret key can alter an existing valid signature for a given public key and message into another signature that is valid for the same key and message.
3. Linearity: Schnorr signatures provide a simple and efficient method that enables multiple collaborating parties to produce a signature that is valid for the sum of their public keys. This is the building block for various higher-level constructions that improve efficiency and privacy, such as multisignatures and others.

ECDSA vs Schnorr

A signature of a message is created using a private key k and consists of 2 numbers: r and s:

Signature(private key, message) = (r, s)

What is meant by malleability of ECDSA, when discussing the advantages of Schnorr, is that a number s can be manipulated, while the signature itself remains valid.

ECDSA:

Private key:   k        (integer)
Public key:    K = k*G  (curve point)
Message:       m        (integer)
Random number: z        (integer)
Calculate:     R = z*G  (curve point)

r - X-coordinate of R
s = (m + r*k)/z         (integer)

Schnorr:

Private key :  k        (integer)
Public key :   K = k*G  (curve point)
Message hash:  m        (integer)
Random number: z        (integer)
Calculate:     R = z*G  (curve point)

r - X-coordinate of R
s = z + Hash(r||K||m)*k (integer)

Where || is a binary concatenation.

It's noticeable that unlike ECDSA there is no division in Schnorr. This small change makes Schnorr signatures linear in nature, and of the generic algebraic form y = a + b*x. This neat property allows us to add two Schnorr signatures, which produces another valid Schnorr signature. In short, now we can do algebra with signatures. This was not possible with ECDSA and it opens a door to more cool cryptographic tricks.

One of the most obvious is multisignatures with Schnorr, which are indistinguishable from regular signatures, known as MuSig. The sum of two individual signatures is also valid for the sum of the individual public keys. Harnessing this property, two parties, Alice and Bob can collaborate and add up their public keys to create one aggregate key. Coins from this public key can then be spent by an aggregate signature:

MuSig:

K(aggr) = K1 + K2 # an aggregated public key
s(aggr) = s1 + s2 # a valid signature for the aggregated public key

Unlike traditional multisignatures which are P2SH, MuSigs are indistinguishable from a plain old P2PKH. The only thing that gets recorded on-chain is a single(aggregated) public key, and a single(aggregated) signature.

So with Taproot, there will be no way to tell whether a transaction is simple P2PKH or P2SH multisig or some other exotic smart contract, they will all look the same. Which obviously adds to anonimity and makes even complex transactions small and simple.

2. BIP341: Taproot — MAST(Merklized Abstract Syntax Trees)

BIP341 describes SegWit version 1 output type, with spending rules based on Schnorr signatures and Merkle branches.

Let's look into a P2SH example:

Encumbrance:
HASH160 <hash of redeem script> EQUAL
Witness:
0 <Sig1> <Sig2> 2 <Pubkey1> <Pubkey2> <Pubkey3> 3 CHECKMULTISIG

This script is huge, because it includes 3 public keys and 2 signatures, but there are even bigger scripts, which consume much more space in the transaction. For example:

Witness:
OP_IF
    <foo>
OP_ELSE
    OP_IF
        <bar>
    OP_ELSE
        <baz>
    OP_ENDIF
OP_ENDIF

Most of the scripts really are just a conjunction of number of possibilities: you can spend UTXO if A and B signed or if C signed and some time passed or D signed and A signed and some hashes revealed etc. Pretty much everything we see today is the combination of these things. And it's sort of unfortunate that we need to reveal all possibilities. Anytime you want to spend anything you need to reveal the complete script.

The observation is that you can instead build a Merkle tree — a hash tree, where leaves combine different scripts together:

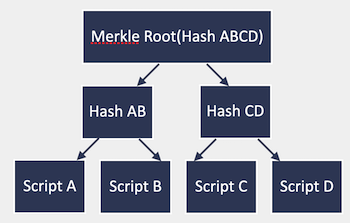
And now in the encumbrance you do not put the script or the hash of the script, but instead the Merkle Root of all the possibilities you want to permit spending.

Encumbrance:
<Pubkey with a Merkle Root(Hash ABCD)>

And then at spending time, as witness you present a path along the Merkle Tree to prove that the output really contained that script and the inputs to the script:

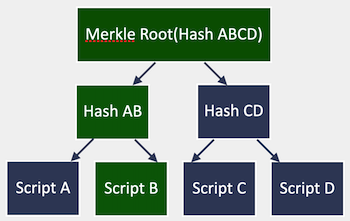
Witness:
<Merkle Root(Hash ABCD) → Hash AB → Script B and inputs>

This has log(n) size in the number of possibilities and you only need to reveal the actually taken branch. This new script type is called Pay to Taproot or P2TR.

Putting this all together BIP341 introduces a SegWit v1 output type which on a surface looks like a normal public key, but can be spent in 2 different ways: it can be either spent using the Schnorr signature, which itself can be an aggregation of the signatures in case of MuSig or it can be unlocked by presenting a solution to one of the branches of the Merkle Tree:

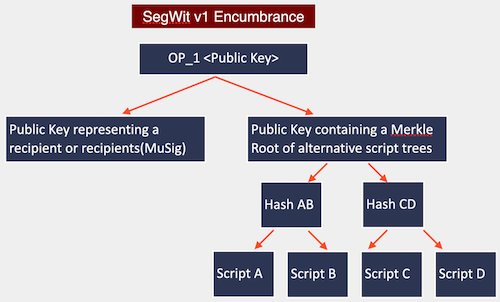
3. BIP342: Tapscript — Validation of Taproot Scripts

Finally BIP342 updates the opcodes for Tapscript:

• OP_CHECKSIG, OP_CHECKSIGVERIFY — modified to verify Schnorr signatures
• OP_CHECKMULTISIG, OP_CHECKMULTISIGVERIFY — disabled in favor of OP_CHECKSIGADD

Conclusions

• Taproot is the 1st update in 4 years and was rolled out in November 2021 as a softfork
• Taproot adds Schnorr signatures in place of ECDSA and this will make complex transactions indistinguishable from the usual P2PKH transactions
• Schnorr signatures together with MAST add to the privacy and limit the amount of exposure of the keys or other spending conditions to the blockchain
• Taproot transactions have the potential to be smaller than traditional Bitcoin transactions, particularly in cases where complex scripts are involved, saving space and reducing fees